Measuring Radiator Flow Rate
with Simple Tools
 |
| The inspiration for Lynn's new method to estimate radiator flow rate—Ike, working on Bugsby's radiator. |
Bugsby's Been Running Hot
Bugsby has been running hot and Lynn is taking steps to try and solve the problem. Through talking with others and thinking about the likely causes, Lynn decides to start with the radiator, having it "boiled" to clean out the mud and crude that have accumulated through the years. Lynn takes the radiator to Pankey's Radiator Shop in Hayward for this service. Ike is the technician at Pankey's who does the work.
When the work is complete, Ike demonstrates to Lynn that the radiator has a good flow rate by plugging the lower outlet hole, filling the radiator to the top, then removing the plug and observing the strength of the flow. This qualitative measure demonstrates that the radiator had a "good" flow rate, but Lynn suddenly realizes that using a little physics he can make this quantitative, computing an absolute flow rate from this simple experiment. The remainder of this page documents this procedure.
Lynn has previously attempted and failed to directly measure the flow rate of the radiator. He attempted to increase the flow from a garden hose until the radiator "backed up," but he found that his garden hose could not supply a strong enough flow to accomplish this. As a result he only established a lower bound on the radiator flow rate, finding that the radiator could flow at least 7 GPM (gallons per minute).
All It Takes is a Little Physics and Mathematics
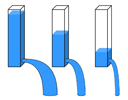 |
| The rate of flow critically depends on the height of the water column above the hole. |
As this diagram attempts to illustrate, the rate of flow of water through a hole depends on the height of the column of water above the hole. (This is the reason that municipal water is stored at the top of a tall tower or at the top of a hill, and how we generate hydroelectricity.) As a result, Ike's method for demonstrating the quality of the flow rate from the radiator doesn't directly give an absolute flow rate since the rate varies during the experiment. What Lynn realizes while watching Ike's demonstration is that this can be related to the elementary physics problem of the leaky bucket. Given a bucket of known dimensions with a hole in the bottom of known area, how long does it take for all the water to escape from the bucket?
Conversely, if we know how long it takes for the water to escape from the bucket, we can compute the effective size of the hole and determine the flow rate for a given height of water in the bucket. What Lynn wants to know is the flow rate when the bucket (radiator) is full.
Yahoo! All he needs to do is take some physical measurements of the radiator (with a tape measure), measure the quantity of water to fill the radiator (with a gallon jug), measure the time for the full radiator to drain empty, and use some elementary physics and calculus to relate the measurements to what he wants to know. Piece of cake!
Bernoulli Knew How to Do It in the Early 1700s
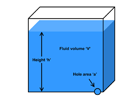 |
| Lynn's leaky bucket model of a radiator. |
Daniel Bernoulli (1700-1782) was a Dutch-Swiss mathematician particularly remembered for his work in fluid mechanics. For subsonic incompressible fluid flows in a uniform gravitational field, Bernoulli's equation states that, anywhere within the fluid flow,
where
 |
Evaluating Bernoulli's equation for the variables at the top of the fluid in the radiator, equating it to Bernoulli's equation for the variables at the outlet hole at the bottom of the radiator, and solving for the difference in pressure in the fluid between the bottom and top of the radiator, we find
Note the remarkable simplicity of this result; the pressure difference only depends on the height of the fluid column and the density of the fluid. The pressure is independent of the details of the shape of the container other than its height.
As a result of this pressure, the water will flow out of the outlet hole with a velocity
In a small increment of time, dt, a small volume of water, dV= a u dt, will escape from the hole of area a. If we sum up (integrate) over the volume of water in the radiator and over the time, τ, it takes for all the water to escape from the radiator, we can compute the effective area of the exit hole.
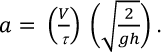 |
We can now evaluate the flow rate (for a full radiator) based on our measurement of the water volume, V, and the time it takes for the radiator to drain, τ, as
If our radiator holds one gallon or water and it takes six seconds (1/10 minute) to drain, the flow rate (when the radiator is full) is not 10 GPM, but twice that according to our equation, or 20 GPM. This makes sense because the water flows quickly at the beginning, but slows down as the level drops in the radiator. Over the time interval τ, we are averaging over a variable flow rate. We're not generally interested in the flow rate when the radiator is half full or almost empty, but our experimental method includes these other flow rates in the measurement.
Alright Already, What's Bugsby's Flow Rate?
 |
 |
 |
 |
| Lynn's equipment and setup to perform his radiator-flow measurement experiment.. | |||
On Feb. 2, 2009, after receiving the cleaned and unpainted radiator back from Ike, Lynn sets up to perform his flow experiment. Lynn plugs the outlet hole with a rubber stopper. Using a calibrated plastic jug, Lynn determines that radiator holds about 2.35+0.05 US gallons. Using a tape measure, he measures the height of the water in the radiator as 26+1 inches.
Lynn performs five trials using the stopwatch on his wrist watch. Discarding the high and low result and averaging the remaining three measurements it takes 10.4+0.2 seconds for the full radiator to empty. Using the equation he derived, Bugsby's full radiator has a measured flow rate of 13.5+0.5 GPM.
What is the effective area of the outlet hole based on this model? Using the known volume of water, drain time, height of the water column and the known acceleration due to gravity, Lynn computes the effective diameter of the outlet hole as 0.969 inches, remarkably close to the one-inch diameter of the actual outlet pipe on Bugsby's radiator. To Lynn this suggests that the outlet pipe is apparently the primary factor limiting the radiator flow rate.
(Lynn makes a mental note. If he needs to increase the radiator flow rate he can consider widening the diameter of the thick-walled outlet pipe on Bugsby's radiator. The current hole diameter is 1" and the outer diameter of the cast pipe is 1.5". If he were to increase the diameter of the hole to 1.25" it would increase the cross sectional area of the outlet by 56%, potentially increasing the flow rate by a similar percentage.)
(For the interested reader that may be checking Lynn's math, be sure that you convert to a consistent set of units for the effective outlet diameter calculation. Recall that the area of a circle is π times the square of one-half of the diameter. Lynn converts everything to SI units, then converts the final result back to inches. In SI units, the 26" height is 0.660 m, the 2.35 gal(US,liquid) volume is 0.00890 m**3, and the acceleration due to gravity is 9.81 m/s**2. He computes the effective diameter of the outlet hole as 0.0246 m.)
The Standard Explanation for Decreasing Flow Rate to Improve Cooling Doesn't Hold Water!
Every now and then, Lynn encounters some really bad science that's gone viral in the car world. For example, it's still often stated that yellow lights make more effective fog lights (due to Rayleigh scattering), but that's just plain hogwash. (See "A Scientific Aside on Yellow Versus White Fog Lights" for more information on this topic.)
A statement that Lynn's been running into recently is that decreasing cooling system flow rate can actually improve the performance of the cooling system. (Lynn's been told this by multiple people at shows and swap meets, and he's seen it in print at least twice. See, for example, Hemmings Classic Car, Vol 3, Issue 11, #35, Aug 2007, p52.) If it is indeed true, Lynn is certain that the explanation that usually given for the result doesn't hold water, scientifically (pun intended).
The explanation for this result goes something like this. If the water flows too rapidly through the radiator, it doesn't have enough time to cool down. By slowing the flow rate, a given quantity of water spends more time in the radiator and transfers more of it's heat to the air, and is cooler when it reenters the block. (Lynn agrees with the argument to this point.) The faulty conclusion is that the cooler water reentering the block cools the engine better. The point that is missed in this argument is that the quantity (gallons per minute) of this cooler water is much lower than that for the warmer water. We have competing factors that bear closer analysis. To understand which of these factors is dominant, we need to understand more about the physics of heat transfer.
It's intuitive once you think about the inverse problem such as heating a cold room with a hot-water radiator. Will the room get warmer faster (is there a higher heat transfer rate) if you dial back the water flow using the inlet valve so that the water leaving the radiator is cooler, or would you open the valve all the way so that the whole radiator is as hot as you can make it? I expect that most people would open the valve (increase the flow rate) to warm the room.
(Note added 2013: Lynn now understands a situation where decreasing the flow rate can improve cooling. In zero-pressure radiators that have an open vent to atmosphere, if the radiator cannot handle the flow being output by the water pump, the excess water will back up and flow out of the vent at the top of the radiator. The lose of coolant will cause the vehicle to overheat. Lynn observed phenomenon with a newly acquired car of his in 2013. When run at high speed, the engine would spit most of it's coolant out of the radiator and then overheat. The former owner of the car had noted frequent loss of coolant and blamed it on a cracked head. Lynn suspects the opposite explanation, that the loss of coolant caused overheating that cracked the head. His solution to the problem was to clean the radiator, seal the radiator with a 4 PSI cap and add an overflow tank.)
To understand the error in the standard explanation for why decreasing-flow-rate-increases-cooling concept, one can use Newton's law of cooling. (That's Sir Isaac Newton, one of the greatest scientists in all of human history, up there with Aristotle, Galileo and Einstein!) This very simple theory states that the rate of heat loss of a body is proportional to the difference in temperatures between the body and its surroundings (environment). Mathematically
where
 |
That is, a gallon of hot water transfers more heat per second to the air than a gallon of lukewarm water. The rate of that transfer is directly proportional to the difference between the temperature of the water and the temperature of the air.
So that's your answer. You loose by slowing down the flow. The cooler water radiates it's heat more slowly than the warmer water. The fewer gallons per minute compounds the problem.
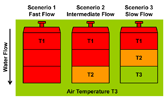 |
| Three radiator flow scenarios are graphically depicted. |
In case that discussion was too opaque, here's another way to look at it. Imagine three scenarios as depicted in the graphic, above.
- The water is moving rapidly and it barely has any time to cool in the radiator. For all practical purposes, the entire radiator is at a single, high temperature, T1.
- The water is moving at some intermediate speed. Roughly, the top 2/3 of the radiator is at the high temperature T1 while the bottom third is at T2, a temperature half way between T1 and air temperature.
- The water is moving still slower. Roughly, the top 1/3 of the radiator is at T1, the middle third is at temperature T2, while the bottom third is at air temperature, T3.
What are the heat transfer rates in these three scenarios according to Newton's law of cooling? For concreteness, let's assume that the hot water temperature T1=190°F, that air temperature T3=70°F, and so T2=(T1+T3)/2=130°F.
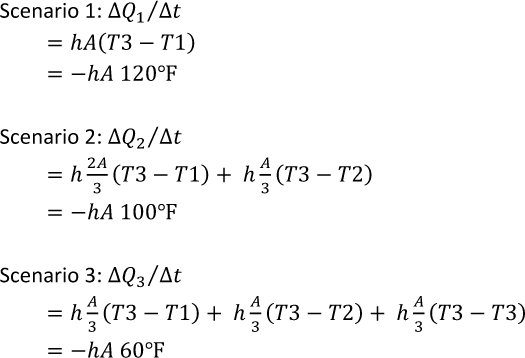 |
Based on our assumed temperatures, Scenarios 2 dissipates heat at a rate about 16% less than Scenarios 1 (100 v. 120). Scenarios 3 dissipates 50% less heat than Scenario 1 (60 v. 120).
Lynn makes an analogy of the cooling system of a car with a conveyor belt. Each gallon of water is like a bucket on the conveyor; it picks up heat in the engine and transports it to the radiator where it is dumped (released) to the air. The rate of heat removed by this conveyor belt is equal to the product of the heat each bucket carries away multiplied by the number of buckets per second whizzing past on the belt. The decreasing-flow-rate-increases-cooling idea increases the amount of heat each bucket carries away, but decreases the number of buckets per second. The cooler the water in each bucket the slower it transfers heat to the air. Lower rate of heat transfer? Fewer number of buckets per second? You lose!
![]()
Contact  with your comments or questions
with your comments or questions
Copyright © 2018 Lynn Kissel
Last updated: Aug. 21, 2013